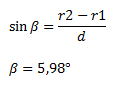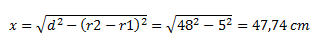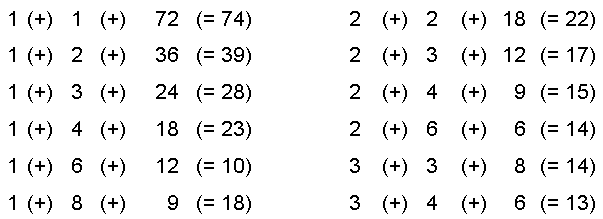Jahr der Mathematik am Institut Dr. Flad
![]()
Das Bundesministerium für Bildung und Forschung (BMBF) veranstaltet seit dem Jahr 2000 zusammen mit der Initiative Wissenschaft im Dialog (WiD) die Wissenschaftsjahre. Gemeinsam mit der Deutsche Telekom Stiftung und der Deutschen Mathematiker-Vereinigung (DMV) wurde 2008 das Jahr der Mathematik ausgerichtet.
Mehr dazu unter www.jahr-der-mathematik.de.
![]()
| |
||||
| Aufgabe des Monats Dezember 2008 | ||||
| Abgabetermin: 31. Dezember 2008 | ||||
| Aufgabe |
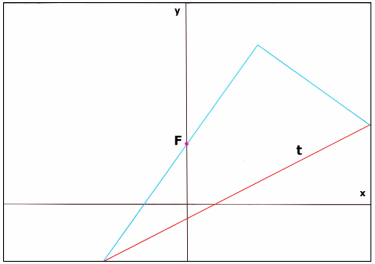
Falten Sie ein DIN-A4-Blatt einmal quer, so dass Sie den Falz y bekommen. Markieren Sie auf y einen Punkt F und falten Sie die Unterkante des Blattes senkrecht nach oben, so dass sie den Punkt F berührt und der Falz x erhalten wird. Messen Sie den Abstand des Punktes F von der Unterkante des Blattes. Wie lautet die Gleichung der Ursprungsparabel p, wenn F ihr Brennpunkt ist und x und y das Koordinatensystem sind?
|
|||
| Lösung | Die Lösung finden Sie im PDF-Format hier. | |||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats November 2008 | ||||
| Abgabetermin: 30. November 2008 | ||||
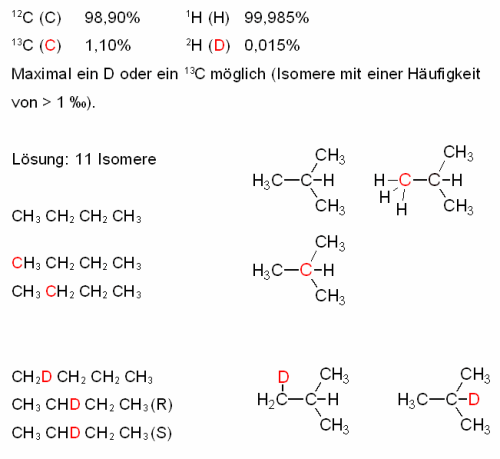
| Aufgabe | Wie viele Isomere gibt es von Butan, wenn man die Isotope 1H, 2H, 12C und 13C und nur Isomere mit einer Häufigkeit von > 1 ‰ berücksichtigt? | |||
| Lösung |
|
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats Oktober 2008 | ||||
| Abgabetermin: 31. Oktober 2008 | ||||
| Aufgabe |
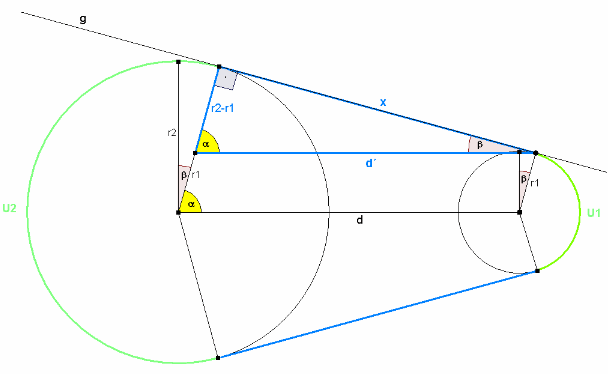
Welche Länge hat eine Fahrradkette, die über das vordere und hintere Zahnrad läuft, wenn sie ganz gespannt ist? Das hintere Zahnrad hat einen Durchmesser von 8,0 cm, das vordere von 18,0 cm und die beiden Naben haben einen Abstand von 48,0 cm. |
|||
| Lösung |
Die Orthogonalen der Tangente g durch die jeweiligen Kreismittelpunkte sind parallel, also haben d und d´ die selbe Länge. Somit lässt sich der Winkel ß über die Sinusfunktion berechnen:
Mit bekanntem Winkel lassen sich die Längen der beiden Kreisbögen bestimmen: 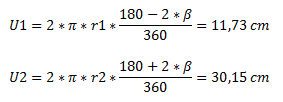 Nach Pythagoras gilt für x:
Gesamtlänge:
|
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats September 2008 | ||||
| Abgabetermin: 30. September 2008 | ||||
| Aufgabe |
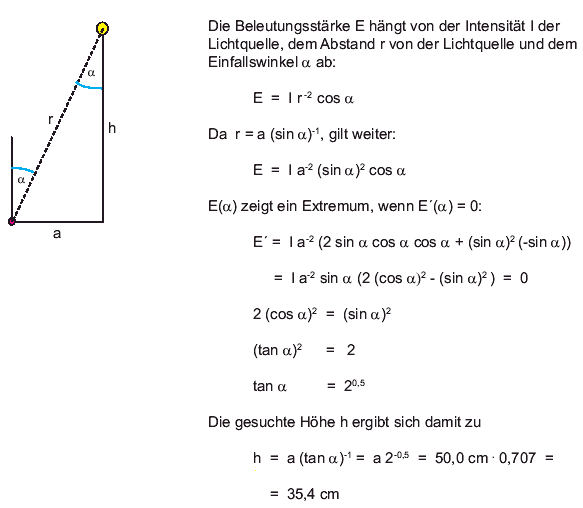
Eine in der Höhe verstellbare Schreibtischlampe steht 50,0 cm von dem zu beleuchtenden Objekt entfernt. Was ist die optimale Höhe der Lampe für eine maximale Ausleuchtung (Helligkeit)? Die Beleuchtungsstärke E nimmt mit dem Quadrat der Entfernung ab, sie ist aber auch vom Einfallswinkel α abhängig (E ~ cos α , bei senkrechtem Lichteinfall wäre α = 0). |
|||
| Lösung |
|
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats August 2008 | ||||
| Abgabetermin: 31. August 2008 | ||||
| Aufgabe |
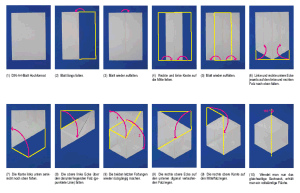
Wie kann man aus einem DIN-A4-Blatt ohne weitere Hilfsmittel ein regelmäßiges Sechseck (wie der Benzolring) falten? Bei verschiedenen Lösungen gewinnt die mit der größten Fläche und der geringsten Anzahl an Faltungen. |
|||
| Lösung | ||||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats Juli 2008 | ||||
| Abgabetermin: 31. Juli 2008 | ||||
| Aufgabe |
Für die Werte 2 und 8 soll das verallgemeinerte Mittel zu 4,5 bestimmt werden. Wie groß ist t? |
|||
| Lösung | t = 0,5 | |||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats Juni 2008 | ||||
| Abgabetermin: 30. Juni 2008 | ||||
| Aufgabe |
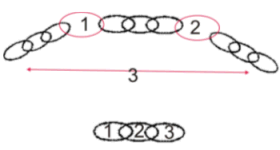
Carola findet im Schmuckkästchen ihrer Großmutter vier Teile eines Goldkettchens, die sie nun vom Goldschmied wieder zu einem ganzen Kettchen zusammensetzen lassen will.
Der Goldschmied sagt zu ihr: " Das Öffnen und das Zusammenlöten eines Kettengliedes kostet 2 Euro."
"Schade", sagt Carola, "ich habe leider nur 7 Euro!". Was ist dem Goldschmied eingefallen? |
|||
| Lösung |
Interessanter Weise besitzen die 4 Teile je 3 Glieder - und das ist der Schlüssel zum Glück! Der Juwelier nimmt sich ein Teil vor und zerlegt es in seine 3 Kettenglieder, die er dazu benutzt, die restliche Kette, die nun aus 3 Teilen besteht, zusammenzuketten und zu verlöten. Preis: öffnen und verlöten von 3 Gliedern zu je 2 Euro = 6 Euro.
|
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats Mai 2008 | ||||
| Abgabetermin: 31. Mai 2008 | ||||
| Aufgabe |
Ein Mann bestellt in einer Gaststätte ein Bier, trinkt es zur Hälfte aus und denkt dann: "Ein Radler (Alsterwasser) wäre doch besser gewesen!" So schüttet er sein Glas nun mit weißer Limonade wieder voll. Er trinkt erneut, diesmal mit weniger Durst und leert das Glas um 1/3. Aber die Geschmacksrichtung scheint noch immer nicht perfekt. Er gießt erneut Limo nach, probiert, indem er 1/6 des Glases leert, ist noch immer nicht zufrieden, kippt das fehlende 1/6 erneut mit Limo nach. Die Geschmacksnerven vibrieren beim Genuss dieses Gemisches. Er trinkt das Glas auf Ex. Hat er mehr Bier oder mehr Limo getrunken? |
|||
| Lösung |
Einem Glas Bier stehen 1/2 + 1/3 + 1/6 Glas Limonade gegenüber: 1/2 + 1/3 + 1/6 = 3/6 + 2/6 + 1/6 = 1 » Die Mengen sind gleich. |
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats April 2008 | ||||
| Abgabetermin: 30. April 2008 | ||||
| Aufgabe |
"Wie breit ist der Fluss eigentlich?" will ein Schüler von seiner Lehrerin wissen, als die Schulklasse auf einer Fähre den Fluss zwischen Ufer A und Ufer B überquert. "Gleichzeitig mit uns legte die entgegenkommende Fähre vom gegenüberliegenden Ufer ab", erklärte die Lehrerin. "Beide Schiffe überqueren den Fluss natürlich auf dem kürzesten Wege, und beide fahren mit konstanter Geschwindigkeit; eine Fähre ist allerdings schneller als die andere. Als wir das entgegenkommende Schiff trafen, waren wir 420 Meter vom Ufer A entfernt. Jede Fähre bleibt nach ihrer Ankunft 10 Minuten liegen, ehe sie wieder zurück fährt. Bei dieser Rückfahrt treffen sich die Boote 260 Meter vor dem Ufer B." Wie breit ist der Fluss? |
|||
| Lösung |
Wenn sich die Fähren zum ersten Mal treffen, haben Sie zusammen gerade so viel Weges zurückgelegt, wie der Fluss breit ist. Wenn sie an dem gegenüber liegenden Ufer ankommen, ist die von beiden Schiffen zurückgelegte Strecke gerade zwei Flussbreiten lang und wenn sie sich auf dem Rückweg treffen, haben sie beide Schiffe zusammen die dreifache Breite des Flusses durchfahren. Da die Geschwindigkeiten konstant sind, muss die Strecke, die jede Fähre beim zweiten Treffen zurückgelegt hat, genau dreimal so lang sein wie der Weg, den sie durchfahren hatten, als die Schiffe sich auf dem Hinweg trafen. Zu diesem Zeitpunkt hatte das von A kommende Schiff 420 m, mithin beim zweiten Treffen 3 mal 420 m zurückgelegt. Das sind 1260 m und das müssen gerade 260 m mehr sein, als der Fluss breit ist, denn beim zweiten Treffen war jene Fähre bereits wieder 260 m vom Ufer B entfernt. Somit ist der Fluss an dieser Stelle genau 1000 m breit. |
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats März 2008 | ||||
| Abgabetermin: 31. März 2008 | ||||
| Aufgabe |
Ein Mathematiklehrer hat 3 Kinder. Ein Schüler fragt ihn nach deren Alter. "Miteinander multipliziert 72". "Addiert geben die Alter meiner Kinder meine Hausnummer". Der Schüler schaut nach der Hausnummer und meint, dass diese Informationen nicht ausreichen. "Wenn meine Frau und ich mal ausgehen, dann passt der älteste auf die anderen beiden auf" fügt er hinzu. Wie alt sind die drei Kinder? |
|||
| Lösung |
Die Zahl 72 lässt sich in Primfaktoren zerlegen: Es gibt also 12 Möglichkeiten für ein Produkt aus 3 Zahlen ... begonnen mit 1, 1, 72 und 1, 2, 36 (beide etwas unwahrscheinlich) bis zur Kombination 3, 4, 6.
2, 6, 6 und 3, 3, 8 haben beide die gleiche Summe 14, deshalb hilft die Hausnummer nicht weiter. Wenn man nun aber davon ausgehen kann, dass es nur ein ältestes Kind geben kann, bleibt genau eine Lösung. |
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats Februar 2008 | ||||
| Abgabetermin: 29. Februar 2008 | ||||
| Aufgabe |
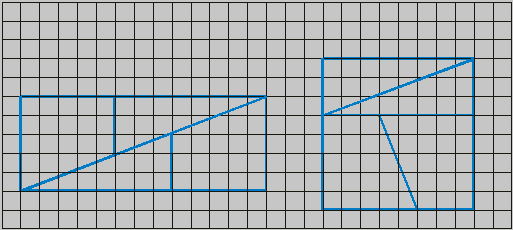
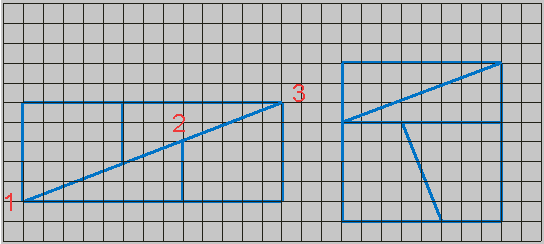
Das Rechteck (links) und das Quadrat (rechts) bestehen jeweils aus zwei Trapezen und zwei rechtwinkligen Dreiecken. Die vier Trapeze und die vier Dreiecke sind offensichtlich gleich groß. Dennoch beträgt die Gesamtfläche des Rechtecks 65 Flächeneinheiten (FE) und die des Quadrats 64 FE. Wie erklärt sich dieser Widerspruch? |
|||
| Lösung |
Die Steigung der Geraden zwischen den Punkten 1 und 2 beträgt 3/8, die Steigung der Geraden zwischen den Punkten 2 und 3 beträgt 2/5. Die Strecke 1-2-3 ist keine Gerade. |
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||
| |
||||
| Aufgabe des Monats Januar 2008 | ||||
| Abgabetermin: 31. Januar 2008 | ||||
| Aufgabe |
x3 - 6x2 + 11x - 6 = 0 |
|||
| Lösung |
L = {1; 2; 3} |
|||
| Preis | Unter den richtigen Einsendungen wurde ein Buchpreis im Wert von 25 € ausgelost. Herzlichen Glückwunsch! | |||