« zurück zur Übersicht - Projektarbeiten
"Riesenseifenblasen"
von Myriam Petit (Schuljahr 2005/06)
| Einleitung | zum Seitenanfang  |
Meine Motivation zum Thema Riesenseifenblasen
Ich fand dieses Thema schon immer interessant, da schon Kinder die Faszination dieser hauchdünnen, schillernden Gebilde entdecken, Erwachsene sich in speziellen Shows begeistern lassen und sogar in der Wissenschaft dienen sie als Vorlagen und Hilfsmittel für einige Versuche. Und wenn schon kleine Seifenblasen so faszinieren, dann die Riesigen ihrer Art erst recht. Es ist fast unglaublich was man alles mit ihnen machen kann.
Trotzdem sehen wir diese Blasen von klein auf als selbstverständlich an und machen uns nie Gedanken darüber, wie sie entstehen, warum sie überhaupt existieren können, zerplatzen oder gar in verschiedenen Farben schillern.
Ich möchte mit dieser Projektarbeit Licht in das Geheimnis dieser zerbrechlichen Kugeln bringen und denke, dass auch nicht chemisch bewandte Personen Gefallen an diesem Thema finden und interessante Kenntnisse erlangen können.
Mein Ziel der Projektarbeit
Ich möchte mit dieser Projektarbeit dem Leser einen Rund Umblick zu dem Thema Riesenseifenblasen verschaffen. Da Riesenseifenblasen dieselben physikalischen und chemischen Eigenschaften wie "normale" Seifenblasen haben, ist diese Projektarbeit auf Seifenblasen aufgebaut. Mein Ziel ist verständlich und übersichtlich dass Geheimnis dieser schillernden Flugobjekte zu lüften und die Selbstverständlichkeit, die ihnen entgegen gebracht wird, in Faszination und Begeisterung für sie zu verwandeln.
Physikalische und chemische Aspekte werden ebenfalls erläutert, wie der Druck in einer Seifenblase, die Oberflächenspannung und der Aufbau einer solchen Kugel, die zum Verständnis notwendig sind.
| 1. Geschichte der Seifenblasen | zum Seitenanfang  |
 Abb. 1 "Seifenbläser" von Jean-Baptiste Siméon Chardin (1699-17779) Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Jean-Baptiste_Siméon_Chardin_022.jpg |
Seit Erfindung der Seife durch die Sumerer vor ca. 5000 Jahren existieren auch die Seifenblasen. Damals fingen die Menschen an, sich wegen der Form, Farbe und Bewegung für Seifenblasen zu begeistern. Die schillernden, dünnwandigen Blasen standen damals schon als Symbol für Zerbrechlichkeit und Vergänglichkeit, vor allem in der Malerei. Das erste Gemälde mit einer Seifenblase entstand bereits im 17. Jahrhundert und ab 1830 wurden Seifenblasen erstmals mathematisch erforscht. 1948. Nach dem Krieg in Deutschland herrschten Hunger und Not im Lande. Aufgrund der Währungsreform war das Geld nichts mehr wert und so blühte der Tauschhandel. Der Chemiker Dr. Rolf Hein experimentierte mit Waschmitteln, die er gegen Lebensmittel bei den Bauern im Umland von Tübingen tauschen wollte. Bei den Versuchen fand er eine Flüssigkeit, die sich aufgrund ihrer Oberflächenspannung sehr gut für Seifenblasen eignete. Dadurch entstand die heute immer noch existierende Firma Pustefix, die mit ihren Seifenblasen Kinder in aller Welt erfreuen. |
In der heutigen Zeit weiß man dass das Experimentieren mit den bunten Wunderkugeln spielerisch das Lernen unterstützt, da das bewusste Erleben und Bestaunen von Naturgesetzen Neugier weckt, Dinge aktiv zu erfahren. Die verschiedenen Formen und Gestalten fördern kreative Potentiale.
Auch in Betreuungsstätten für Behinderten fördern sie die Therapie und im Krankenhaus wird mit ihnen, zu Rehabilitationszwecken, Bewegungsmotorik und Atemübungen durchgeführt.
Heutzutage werden die Seifenblasen sogar von der Wissenschaft genutzt, als Vorlage und Anregung für Bauwerke.
| 2. Entstehung der Seifenblase | zum Seitenanfang  |
Allgemein gesehen entstehen Seifenblasen aus:
- Wasser (am besten destilliertes Wasser)
- Tenside (Waschaktive Substanzen, welche die Oberflächenspannung vermindern, z. B. Spülmittel)
- Verdickungsmittel (z. B. Glycerin, Zucker)
Für die Entstehung einer Seifenblase sind in erster Linie die Tenside nötig. Es gibt anionische, nichtionische, kationische und amphotere Tenside:
Neben der unpolaren Kohlenwasserstoffkette haben anionische Tenside ein negativ geladenes Kopfteil, sind somit hydrophil und eignen sich besonders zum Lösen von Schmutz (hydrophob).
Seifen sind anionische Tenside, die sehr empfindlich auf Magnesium- und Calciumionen in hartem Wasser reagieren. Das heißt, dass die Reaktion mit diesen Ionen im Vergleich zu der Anlagerung an Schmutzpartikel bevorzugt eingegangen wird und so weniger Waschwirkung erfolgt.
In modernen Waschmitteln machen sie den größten Anteil an waschaktiven Substanzen aus.
Allgemein gesprochen, haben Tenside ein polares Kopfteil und ein unpolares Kohlenwasserstoffende, dass hier durch symbolisiert werden soll.
Aufbau einer Seifenlamelle:
Die hydrophoben Enden stehen zueinander. So bildet sich eine Mizelle. Zwischen der flüssigen und der gasförmigen Phase bildet sich auf der Oberfläche eine Schicht aus Mizellen. Dadurch wird die Oberflächenspannung des Wassers herabgesetzt.
Die Wassermoleküle befinden sich im Inneren der Flüssigkeit. An der Oberfläche der Lauge sind die Seifenanionen mit ihrem negativen Enden nach innen gerichtet. Ihre wasserabweisende (hydrophobe) Seite zeigt aus der Seifenlauge hinaus. Die wasserliebende (hydrophile) Seite setzt die Oberflächenspannung des Wassers herab und es bildet sich eine einseitige Membran.
Wenn man diese Membran mit einem Draht anhebt, bildet sich sofort eine Doppelmembran (bimolekulare Tensidschicht, Lamelle).
Das bedeutet man fängt Wasser zwischen den beiden Membranen ein. Die wasserliebende Seite hält das Wasser fest.
Wird nun Luft in die Lamelle geblasen, dehnt sich die Membran soweit, bis sich ein optimales Verhältnis zwischen Oberfläche und Inhalt gebildet hat. Dann kann sich die Seifenblase vom Pustering lösen.
Seifenschaum entsteht wenn mehrere Seifenblasen sich vereinen. Die hydrophoben Schwanzteile treffen dabei aufeinander und stellen den Kontakt zur Nachbarseifenblase her.
| 3. Warum zerplatzen Seifenblasen so schnell? | zum Seitenanfang  |
Durch den Überdruck in einer Seifenblase und die regelmäßige Anordnung der Tensidmoleküle herrscht eine gewisse Stabilität in der Blase. Doch die Seifenlauge in der Blase läuft aus Gründen der Schwerkraft immer weiter nach unten, welches gut an den bunten Schlieren erkennbar ist. Da am oberen Teil der Blase wesentliche Anteile des Wassergehaltes verdunsten verdünnt dieser sich immer mehr, bis er platzt. Beim Zerplatzen treten die gleichpoligen Enden der Tensidmoleküle in Wechselwirkung und stoßen sich ab. Dadurch zerplatzt die Blase. Die meisten Seifenblasen zerplatzen im oberen Teil , einige aber auch am unteren. Wenn man eine Seifenblase in ein Einmachglas sperrt kann man das Verdunsten behindern, und somit die Lebensdauer der Blase verlängern.
Beim Aufeinandertreffen zweier Seifenblasen oder wenn man sie mit dem Finger berührt, werden die Tensidmoleküle durch ihre gleiche Ladung verdrängt, was bedeutet, dass die Konzentration der Moleküle abnimmt. Dies bewirkt eine Vergrößerung der Oberflächenspannung. Die Kräfte im Inneren der Blase versuchen dies durch Kontraktion auszugleichen. Somit ist der Gasdruck in der Seifenblase zu hoch und sie zerplatzt. Beim Zerplatzen einer Seifenblase wird die gesamte zum Aufblasen notwendige Energie in Bruchteilen von einer Sekunde in die Bewegung der Tröpfchen gesteckt. Daher ist dann das Herumspritzen von unzählig vielen Laugentröpfchen zu beobachten.
| 4. Farben von Seifenblasen | zum Seitenanfang  |
 Abb. 11 "Farbkreis nach Johannes Itten (1961)" © Malte Ahrens Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Farbkreis_Itten_1961.png |
Wir haben uns so an Farben und Licht gewöhnt dass wir sie als selbstverständlich hinnehmen, und manchmal vergessen wie stark sie unser Leben bestimmen. Ohne Licht wäre kein Leben auf der Erde möglich. Physikalisch ist Licht als elektromagnetische Strahlung mit hoher Energie definiert. Licht ist also Energie, die in verschiedenen Wellenlängen schwingt.
Licht besteht aus schwingenden Strahlen, wobei energiereichere Strahlen kurzwellig sind und eine hohe Frequenz haben.
Bohr entdeckte, dass Elektronen für die Erzeugung von Licht verantwortlich sind. Er fand heraus, dass die auf Teilchen übertragene Energie (z.B. durch Wärme) auf die in Bahnen um den Atomkern kreisende Elektronen des jeweiligen Atoms übergehen. Wenn ein Elektron einen "Energiestoß" bekommt springt es auf eine vom Atomkern entfernte Bahn. Hier hält sich das Elektron nur kurz da dieser Zustand nicht stabil ist. Sobald der Energiestoß vorüber ist springt es wieder zurück auf seinen alten Platz. Die zuvor aufgenommene Energie wird dabei in Form von Licht frei. Dieser Vorgang findet nicht nur einmal statt und es werden dabei mehrere Elektronen angeregt, deshalb spricht man auch vom "Schwingen der Atome". Je nachdem wie groß die Energie ist, die einem Elektron zugefügt wird, desto schneller schwingen die Atome.
Licht wird durch die Frequenz und die Wellenlänge der Schwingungen beschrieben. Wenn wir eine andere Farbe sehen ändert sich die Wellenlänge des Lichts. Von der Sonne erhalten wir Sichtbares Licht. Es schwingt mit einer Wellenlänge von 400 bis 800nm. Dies ist der Vis-Bereich (Vis: engl. Visible = sichtbar).
Nimmt man nun aus diesem Bereich eine ganz bestimmte Wellenlänge heraus, sehen wir Farben. Dies kann u.a. durch Lichtbrechung geschehen. Ein Beispiel der Lichtbrechung, das bestimmt jeder kennt ist der Regenbogen. Das Licht wird durch die Regentropfen zerlegt, das menschliche Auge kann jetzt verschiedene Farben wahrnehmen.
Wir sehen immer die Komplementärfarbe des herausgefilterten Lichts.
Farben von Seifenblasen sind Interferenzerscheinungen. Trifft das Licht auf die zwei Oberflächen der Tensidschicht, so wird es an der äußeren, wie inneren Seite teilweise gebrochen und teilweise reflektiert. Somit muss der auf die innere Seite auftreffende Strahl einen längeren Weg zu unserem Auge zurück legen.
Der "längere Strahl" schwingt so mit anderer Frequenz (= 1/Wellenlänge) als der kürzere. Aufgrund dieser unterschiedlichen Wellenlängen sehen wir eine Farbe.
Eine Seifenblase besteht aus einer ungleichmäßig dicken Schicht, was durch das allmählich nach unten fließende Wasser zwischen den Tensidschichten hervorgerufen wird, dadurch reflektiert ständig eine andere Wellenlänge oder sie wird ganz ausgelöscht. Die Seifenhaut muss ständig in Bewegung sein, um den Konzentrationsunterschied der Tenside an der Oberfläche auszugleichen. Dadurch schillern Seifenblasen.
Wenn die Wand der Seifenblase relativ dick ist , werden mehr rote Lichtwellen ausgelöscht, wodurch man eine blau-grüne Färbung sehen kann. Mit abnehmender Dicke verändert sich die Farbe ins bläuliche, dann ins rötliche und schließlich wird sie gelb. Wenn die Dicke der Wand kleiner ist als die Hälfte der Wellenlänge des sichtbaren Lichts, löschen sich keine sichtbaren Wellenlängen gegenseitig aus und es können keine Komplementärfarben mehr wahrgenommen werden. Die Seifenblase ist nun dünner als zwei Zehntausendstel eines Millimeters und steht kurz vor dem Zerplatzen. Ist die Haut der Seifenblase an einer Stelle allerdings "dicker" als 1/1000 mm erscheint die Seifenblase durchsichtig. Dies liegt daran, dass sich das reflektierte Licht zweier dicht nebeneinander auf die Seifenhaut auftreffenden Strahlen überlagert und sich so die Farben gegenseitig aufheben.
Wenn eine Seifenblase überall die gleiche Wandstärke hätte wäre sie einfarbig.
Eine Seifenblase ist durchschnittlich1 µm dick. Für jede Spektralfarbe kann eine Schichtdicke errechnet werden. Formel zur Berechnung der Auslöschbedingungen:
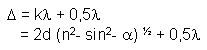
Legende:
Δ = Gangunterschied der jeweiligen Teilwelle
k = Wellenzahl (Zahl der entstandenen Zahlen)
λ = Wellenlänge
d = Schichtdicke der Seifenhaut
n = Brechungsindex
α = Einfallswinkel
Einer der beiden Strahlen (hier b) ist länger als der andere = Gangunterschied

Abb. 13 "Two soap bubbles" © en:User:Tagishsimon
Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Soap_Bubble_-_foliage_background_-_iridescent_colours_-_Traquair_040801.jpg
| 5. Pusteringe selber machen | zum Seitenanfang  |
Pusteringe können leicht selbst hergestellt werden, indem man einen Draht kreisförmig biegt, die Enden miteinander verbindet und diesen mit einem Baumwollfaden eng und gleichmäßig umwickelt. Dadurch kann sich die Lamelle sehr gut ausbilden wenn in der Wolle genügend Seifenlauge gesammelt ist.
In Größe und Form können die Pusteringe variiert werden, so dass sogar Würfel, Pyramiden und ähnliche Figuren gebogen werden können. Möchte man eine große Blase entstehen lassen ist es etwas problematisch die Seifenlamelle in den Ring zu spannen. Das Gestell sollte deshalb hochkant nach oben aus der Seifenlösung gezogen werden und anschließend kurz abtropfen. Bei kleineren Pusteringen vorsichtig in das untere Drittel der Lamelle blasen, bei den Größeren ist es ratsam sie durch eine gleichmäßige Bewegung durch die Luft zu ziehen. Zum Ablösen der Blase sollte eine sanfte Handdrehung (S-Form) folgen.
| 6. Seifenblasen und Mathematik | zum Seitenanfang  |
Seifenblasen sind tatsächlich auch mathematisch interessant. Mathematiker wissen von Physikern, welche Kräfte auf eine Seifenbase wirken - Spannungskräfte zwischen Molekülen der Seifenhaut, die so wirken, dass die Oberfläche der Blase möglichst klein wird. Denn ein Seifenfilm formt eine natürliche Minimalfläche.
Deshalb helfen Seifenblasen der Mathematik, beim Lösen komplexer räumlicher Probleme, da sie jederzeit die kleinste Oberfläche zwischen Punkten und Kanten bilden.
Wie die Oberfläche einer Seifenblase aussieht, ist mathematisch gesehen ein so genanntes Minimierungsproblem. Die Oberfläche soll so klein wie möglich sein, mit der Nebenbedingung dass das Volumen so groß wie möglich dabei sein soll. Mathematiker kennen dafür allgemeine Methoden, die zur so genannten Variationsrechnung gehören, und können eine Gleichung ableiten, der die gesuchten Oberflächen genügen müssen. Wenn man diese Gleichungen untersucht, lässt sich beweisen, dass die einzigen möglichen Lösungen im herkömmlichen Raum (genauer: im euklidischen Raum) Sphären sind, also die Oberflächen von Kugeln. Dies ist der mathematische Grund, warum Seifenblasen rund sind. Diese Lösung gilt bei uns auf der Erde nur näherungsweise, denn beispielsweise der Effekt der Erdanziehungskraft ist in diesem Modell noch nicht berücksichtigt. Allerdings müsste eine Seifenblase in einer Raumstation, fern aller Massen und ihrer Gravitationseinflüsse, exakt rund sein.
Ein Seifenfilm formt eine natürliche Minimalfläche. Komplizierter wird das Problem, wenn ein Drahtgebilde in eine Seifenlauge eingetaucht wird - welche Form hat die Seifenhaut, die sich innerhalb des Drahts ausbildet dann? Die Experimente des belgischen Physikers Joseph Plateau lieferten dazu eine wesentlichen Beitrag.
Nach diesem Physiker ist auch das Plateau-Problem benannt. Mathematisch gesehen handelt es sich wieder um ein Minimierungsproblem, hier allerdings mit einer Randbedingungen - die gesuchte Seifenhaut soll auf einem ganz bestimmten Drahtgebilde enden. Minimalflächen sind Flächen die dieses Problem lösen.
Herrmann Amandus Schwarz bewies 1884 , dass eine kugelförmige Seifenblase die kleinstmögliche Oberfläche eines bestimmten Luftvolumens besitzt. Professor Joel Hass und Roger Schlafly gelang es 2000 zu beweisen, dass zwei verbundene Seifenblasen die kleinstmögliche Oberfläche zweier umschlossener Luftvolumen haben (Doppel-Blasen-Theorem).
| 7. Seifenblasen als Forschungsobjekte in der Wissenschaft | zum Seitenanfang  |
Seit den 50er Jahren experimentierten auch Architekten mit Seifenblasen um Lösungen für extrem materialsparende Bauten zu entwickeln. Sie nutzten die natürliche Form der Seifenhäute als Vorbild für stabile und sichere Baukonstruktionen. Ein Beispiel hierfür ist das Zeltdach des 1972 eröffneten Olympiastadions in München. Es besteht aus einem Netz aus Stahlseilen, in dessen Felder Acrylglasplatten eingesetzt sind. Aus der Ferne erinnert die Dachkonstruktion an eine gigantische Seifenhaut, der sie auch tatsächlich nachempfunden ist.
Taucht man einen dreidimensionalen Stahlrahmen in Seifenlauge nimmt die Seifenhaut aufgrund des Minimalflächenprinzips automatisch die kleinstmögliche Form an. Diese ist für Architekten deshalb so interessant, weil sie gleichzeitig die optimale, sicherste und stabilste Grundform ist.
Durch Minimalflächenversuche wurden auch kürzeste Straßen- oder Telefonnetze zwischen einer Anzahl von Orten ermittelt.

Auch das Dach des Olympiastadions wurde mit Hilfe von Drahtrahmen und Seifenhäuten ausprobiert, anschließend wurden die Seifenhäute vermessen und maßstabsgerecht übertragen.
Abb. 16 "Olympiahalle " © Radox; Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Olympiahalle.jpg
| 8. Physikalische Erklärungen zum Minimalflächenprinzip | zum Seitenanfang  |
 Abb.18 "Struktur von Seifenblasen" © André Karwath aka Aka Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Foam_-_big.jpg |
Seifenblasen stellen fast perfekt physikalische Modelle dar. Sie sind nach ganz bestimmten geometrischen Grundeigenschaften aufgebaut. Ein anderes Minimalprinzip ist das Le Chatelier-Braun'sches Prinzip des kleinsten Zwanges. Auch die Bienenwabe ist ein Beispiel für das Minimalflächenprinzip. Die Bienenwaben sind so aneinander gereiht, dass bei minimaler Fläche mit dem kleinsten Wachsverbrauch ein größt möglichstes Volumen erreicht wird. Wenn die Waben kugelförmig wären, würden zwischen den einzelnen Waben viele Abstände entstehen, die nicht genutzt werden könnten. |
| 9. Grundregeln für Minimalflächen | zum Seitenanfang  |
- Minimalflächen stoßen stets senkrecht an feste Oberflächen.
- Drei aufeinander treffende Minimalflächen bilden stets Winkel von 120°.
Stoßen mehr als drei Minimalflächen aneinander so schneiden sie sich stets in einem Punkt, je zwei Schnittlinien treffen sich unter dem Winkel 109° 28' 16''
Im 19. Jahrhundert von Plateau experimentell herausgefunden, erst 1976 von Algren und Taylor mathematisch bewiesen.
Wenn zwei gleich große Seifenblasen zusammengeführt werden, bilden sie in der Mitte eine Trennwand, die eine ebene Fläche bildet. Weil der Innendruck kleinere Seifenblasen stets höher ist, ragt bei zwei unterschiedlich großen Seifenblasen immer die Kleinere in die Größere hinein.
Jakob Steiner (Mathematiker) behandelte erst vor wenigen Jahren dass Problem, die kürzeste Verbindung zwischen zwei Punkten zu finden. Die Lösung hängt von der Lage der Punkte ab. Wenn drei Punkte so liegen, dass sie ein gleichseitiges Dreieck bilden, ist der Weg der Außenkanten 13 % länger als ein Weg im Inneren des Dreiecks, bei dem sich die Verbindungslinien mit einem Winkel von 120° treffen.
Es gibt verschiedene Arten von Minimalflächen. Eine Kugel bildet den größten Inhalt mit minimaler Fläche.
Das Phänomen des kürzesten Weges kann, statt durch kompliziertes Rechnen, was bekanntlich extrem zeitaufwendig ist, auch experimentell bewiesen werden:
Versuch zum Thema Minimalflächen
Das Ziel dieses Versuchs ist die Demonstration von Minimalflächen von Seifenlamellen.
Es werden ein Würfel und Ring aus Draht für gleichförmige, und ein Styroporklotz mit Nägeln (um die Nähfaden gespannt ist) für ungleichförmige Seifenflächen hergestellt und in Seifenlauge getaucht.
Aufbau: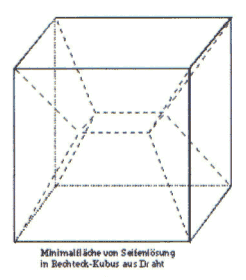 Abb. 23 |
 Abb. 24 |
Nun taucht man den Würfel in die Seifenlösung. Man kann sofort die Bildung der Minimalfläche erkennen.
Aufgrund der Oberflächenspannung nehmen die Seifenhäute, nach dem Minimalflächenprinzip, die kleinste, und damit energetisch günstigste Fläche, bei größtmöglichem Volumen ein.
Wird der Kreisring in die Seifenlösung getaucht und wieder herausgeholt, so bildet sich eine Lamelle, in welcher der Faden frei schwimmt. Da die Position des Fadens keinen Einfluss auf die Größe der Gesamtoberfläche hat, ist der Faden beweglich. Es herrscht ein Kräftegleichgewicht. Durch die Viskosität der Lösung bewegt er sich langsamer als an der Luft.
Wenn man nun die eine Hälfte der Lamelle zersticht zieht sich die noch intakte Lamelle zusammen und der Faden schnellt nach oben, da die Gegenkraft durch die untere Lamelle fehlt. Dies geschieht natürlich genau umgekehrt, wenn man statt der Unteren, die obere Seifenhaut zerstört. Die Gewichtskraft ist also im Vergleich zu der Kraft der Oberflächenspannung klein.
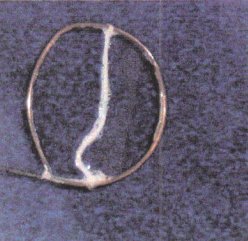 Abb. 28 Faden schwimmt in der intakten Lamelle. |
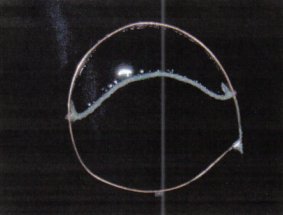 Abb. 29 Lamelle nimmt die kleinste Oberfläche ein. |
In den Styroporklotz werden mit unterschiedlicher Tiefe lange Nägel gesteckt um die Nähfaden gespannt wird. Nach dem Eintauchen in die Seifenlauge können die Minimalflächen dynamisch verändert werden, indem man die Nägel reinschiebt oder rauszieht.
 Abb. 30 |
 Abb. 31 |
| 10. Die Oberflächenspannung | zum Seitenanfang  |
Aufgrund ihrer Polarität ziehen sich Wassermoleküle an. Diese Anziehungskraft wirkt nur im innerhalb des Wassers sobald sie an der Grenzfläche zu einer anderen Phase (Fett, Luft) wirkt. Die zwischenmolekularen Kräfte heben sich innerhalb der Phase auf, da die Moleküle auf allen Seiten von ihresgleichen umgeben sind. An einer Grenzfläche sind diese Kräfte nicht ausgeglichen.
Eine in das Phaseninnere gerichtete Kraft zieht die Moleküle von der Phasenoberfläche in ihr Inneres, wodurch eine Spannung entsteht, welche Oberflächenspannung genannt wird.
Die Oberfläche einer Flüssigkeit ist energiereicher als ihr Inneres. Wasser hat eine sehr hohe Oberflächenspannung, die durch Tensidmoleküle herabgesetzt werden kann, da sie durch ihre Anwesenheit die Anziehung zwischen den Wassermolekülen behindern, und so die Oberflächenspannung herabsetzen. Bei Seifenblasen muss die Oberflächenspannung um ca. 2/3 verringert sein, da die Blase durch die zu hohe Spannung sofort platzen würde. Zusätzlich verlangsamt die Seife die Verdunstung und verlängert so die Lebenszeit einer Seifenblase.
| 11. Versuche: Herstellung verschiedener Seifenlösungen | zum Seitenanfang  |
| 11-1. Lösungen mit denen es nicht so gut geklappt hat | zum Seitenanfang  |
| Nr. 1 |
|
Auch durch Veränderung der Konzentration an Spülmittel war keine Blasenbildung möglich |
| Nr. 2 |
|
Versuch möglichst viele stabilisierende Mittel zu vereinen schlug fehl, da die Lösung zu dickflüssig war. Trotz Verdünnung bildeten sich keine Seifenblasen. |
| Nr. 3 |
|
Vereinzelte Blasen kamen zustande, die jedoch sehr schnell wieder zerplatzten. An der Farbe war zu erkennen, dass die Blasenhaut sehr dünn war. |
| Nr. 4 |
|
Versuch Glycerin durch Maissirup zu ersetzen schlug fehl, da fast keine Blasen entstanden. |
| Nr. 5 |
|
Es kamen keine Blasen zustande. |
| Nr. 6 |
|
Die Seife gab nicht lösbare Klumpen und es war nicht möglich eine Seifenlösung herzustellen. |
| 11-2. Gelungene Seifenlösungen | zum Seitenanfang  |
| Nr. 1 |
|
Blasen waren extrem stabil. Es bildeten sich meist mittelgroße Blasen, die leicht schillerten. Abb. 33 |
| Nr. 2 |
|
Es war schwer Blasen zu bilden. Es bildeten sich teilweise kleine Seifenblasen. Große Blasen konnten sich dagegen nicht so lange halten. Die Seifenblasenhaut blieb als Rückstand zurück. Abb. 34 |
| Nr. 3 |
|
Beste Seifenblasen wurden erzielt. Sie waren groß, schillerten und waren sehr stabil. Die längste gemessene Zeit, die solch eine Blase existierte, betrug 3 Minuten und 30 Sekunden. Zum Vergleich: die längste gemessene Zeit bei den anderen Lösungen betrug ca. 15-20 Sekunden Abb. 35 |
| 11-3. Riesenseifenblasen | zum Seitenanfang  |
- 1,5 Liter destilliertes Wasser (d&m)
- 200 ml Maissirup (www.raabvitalfood.de)
- 450 ml Geschirrspülmittel (grünes "alio" Spülmittel)
Alle Zutaten mindestens 4 Stunden ruhen lassen.
|
|
|
| 11-4. Lösungen mit Polyethylenglykol-Zusätzen (PEG) | zum Seitenanfang  |
Die Idee war durch PEG-Zusätze die Blasengröße zu verändern.
Dabei war die Überlegung durch größere Kettenlängen größere Seifenblasen zu erzielen.
- 3g PEG
- 20g Spülmittel
- 10g Zucker
- 100 ml destilliertes Wasser
Die Zahlen der PEG-Lösungen geben jeweils die Kettenlängen an.
- PEG 4000: Keine gute Blasenbildung. Wenn, dann nur sehr kurzlebige Blasen.
- PEG 6000: Blasen schlossen sich sehr schlecht.
Auswertung:
Der Versuch ergab kein klares Ergebnis. Durch Vergleichen der Brechungsindizes sollen nun weitere Unterschiede festgestellt werden.
Messung der Brechungsindizes nD20
nD20: Brechungsindex bei 20°C der Natrium-D-Linie bei der Wellenlänge von 589 nm. Der Brechungsindex ist abhängig von der Temperatur, der Wellenlänge und der optischen Dichte des Stoffes. Er wird mit Hilfe eines Refraktometers gemessen.

Auswertung:
Der Brechungsindex bleibt fast konstant, d.h. keine konkrete Veränderung der Seifenlösung ist festzustellen. Anhand der Messergebnisse erkennt man, dass es uninteressant ist welche PEG-Zusätze zugegeben werden.
| 12. Haltbarkeit der Seifenblasen | zum Seitenanfang  |
- Lösung 1: mittlere Blasen ca. 20 Sekunden
- Lösung 2: mittlere Blasen ca. 15 Sekunden
- Lösung 3: mittlere Blasen ca. 3 Minuten und 30 Sekunden
Generell sind kleinere Seifenblasen länger haltbar und stabiler als Große. Genaue Angaben sind aus Problemen der Reproduzierbarkeit (d.h. kein konstantes Volumen, ungleiche Messbedingungen, Witterung, Temperatur, Druck) nicht möglich.
Rückstände der Lösungen
Die Rückstände der Lösungen 1 und 2 ließen sich nur schwer unterscheiden. Bei beiden blieben leichte Reste zurück. Die Seifenblasen der Lösung 3 zerplatzten meist nicht richtig, sondern verloren nur Luft. Die Blasenhaut blieb fast vollständig erhalten, was auf eine sehr große Stabilität der Seifenblasenoberfläche schließen lässt.
| 13. Allgemeine Hinweise | zum Seitenanfang  |
Die eingesetzten Stoffe sind in kleinen Mengen ungefährlich. Alle Lösungen wurden mit unbestimmten Zusammensetzungen getestet um Seifenblasen herzustellen, die möglichst stabil und haltbar sind. Lösungen mit Tapetenkleister sollten über Nacht stehen gelassen werden. Zuviel Schaum in den Seifenlösungen verschlechtert die Qualität der Blasen und erschwert die Lamellenbildung. Methylcellulose ist das im Tapetenkleister enthaltene wichtige Mittel für die Verdickung. Die Seifenblasenlösungen können problemlos von jedem hergestellt werden, da man sogar Glycerin in Apotheken kaufen kann.
| 14. Versuche zum Thema Oberflächenspannung | zum Seitenanfang  |
Das Ziel dieses Versuchs ist die Demonstration der Oberflächenspannung einer Seifenlösung.
Der Versuch wurde mit der Lösung 3 durchgeführt, da mit dieser die besten Seifenblasen erzielt wurden.
Ein Draht wird hierzu u-förmig gebogen und ein beweglicher Bügel angebracht. Die Apparatur wird in Seifenlösung getaucht, wieder herausgeholt und mit der offenen Seite des Bügels nach unten gehalten. Der Bügel kann nun entlang der Drahtenden nach unten bewegt werden. Eine Kraft ist hierzu nötig, da die Oberfläche der Seifenlamelle vergrößert werden muss. Ohne äußere Krafteinwirkung hängt der Bügel ganz oben. Durch ein Gewicht am Bügel kann dieser in jeder Position "schweben". Ohne Gewicht würde er immer wieder nach oben schnellen.
Aufbau: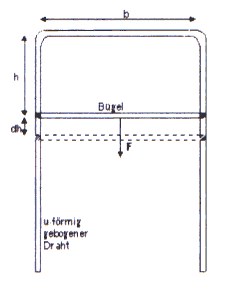 Abb. 39 |
 Abb. 40 |
 Abb. 41 |
 Abb. 42 |
Auswertung:
Da die Moleküle an der Oberfläche eine höhere Energie als im Inneren haben, möchte die Seifenlösung eine möglichst kleine Oberfläche bilden. Bei dem durchgeführten Versuch wirkt die Oberflächenspannung der Gewichtskraft entgegen und zieht den Bügel hoch. Die Kraft F ist unabhängig von der Verschiebung h.
Gewicht am Bügel (F) = 0,18 g
Länge des Bügels (b) = 9,3 cm
Formel zur Berechnung der Oberflächenspannung:
σ = F/2b
σ = 1,29 g / 2 x 9,3 cm
σ = 0,069 g/cm
Die Oberflächenspannung der Lösung 3 beträgt 0,069 g/cm.
Der nächste Versuch dient zu qualitativen Messung einer Flüssigkeit.
Dazu braucht man einen Ring der an einem Faden hängt und mit diesem vertikal bewegt werden kann. Die Flüssigkeit , in die er getaucht wird, steht auf einer Waage. Man zieht ihn langsam wieder raus und beobachtet die Gewichtsabnahme.
Aufbau: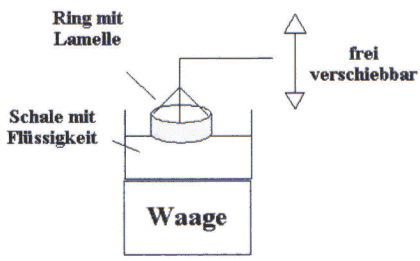
Abb. 43
Auswertung:
Gewichtsabnahme an der Waage (F) = 2,17 g
Radius des Ringes = 2,5 cm
Formel für die Berechnung der Oberflächenspannung:
F = 4π x r x s
σ = 2,17 g / (4π x 2,5 cm)
σ = 0,069 g/cm
 Abb. 44 |
 Abb. 45 |
| 15. Druck in einer Seifenblase | zum Seitenanfang  |
In Seifenblasen herrscht ein Überdruck, der auch für ihre Stabilität verantwortlich ist. Um so größer der Radius der Seifenblase ist, um so größer ist auch der darin vorhandene Überdruck. Daher kann eine größere Blase von einer kleineren aufgeblasen werden. Treffen eine große und eine kleine Seifenblase aufeinander so sieht man, dass die Kleine in die Große hineinragt. Wird der Überdruck in der Seifenblase zu klein, zerplatzt diese auch.
Versuch zum Thema Druck in der Blase
Ziel des Versuches ist es den Druck in einer Seifenblase zu ermitteln.
Zwei Rohre werden dazu über ein Ventil miteinander verbunden. An beide Rohre wird eine Seifenblase unterschiedlicher Größe angebracht. Die Ventile werden nach dem Lufteinlassen verschlossen, und die Verbindung zwischen den beiden Rohren geöffnet. Es findet ein Druckausgleich zwischen den beiden Blasen statt, indem die Kleine die Große aufbläst. Dies geschieht solange, bis die kleine Seifenblase verschwunden ist.
Aufbau: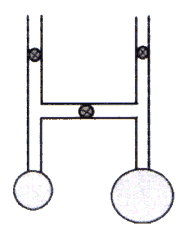
Abb. 46
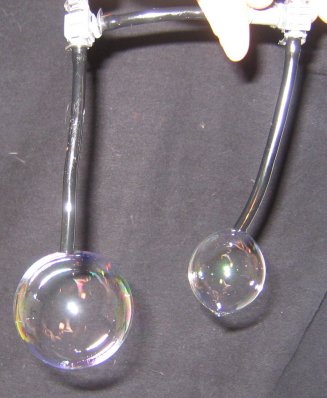 Abb. 47 |
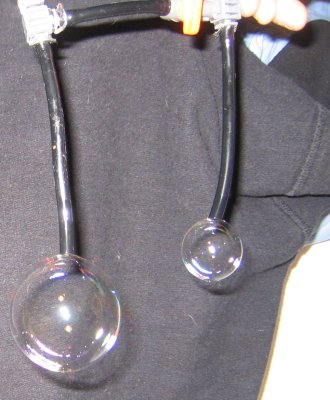 Abb. 48 |
Auswertung:
Der Druck in der Seifenblase kann berechnet werden.
Formel zur Berechnung des Überdrucks in einer Seifenblase:
Δp = 4π / r
Radius der großen Blase (r1) = 4,0 cm
Radius der kleinen Blase (r2) = 2,5 cm
| Berechnung des Drucks in großen Seifenblasen: | Δp | = | 4π / 4,0 cm |
| Δp | = | 3,1 mbar | |
| p | = | Δp + 1013 bar | |
| p | = | 4,113 mbar | |
| Berechnung des Drucks in der kleinen Blase: | Δp | = | 4π / 2,5 cm |
| Δp | = | 5,0 mbar | |
| p | = | Δp + 1013 bar | |
| p | = | 6,013 mbar | |
Anhand dieses Versuches und der Berechnung der Einzeldrücke wird ersichtlich, dass der Druck in der kleinen Blase größer ist und sie deshalb zum Druckausgleich die Größere aufblasen muss.
| 16. Faszinierende Anwendungsversuche mit Seifenblasen | zum Seitenanfang  |
| 16-1. Schaumsäule | zum Seitenanfang  |
In einen großen Standzylinder gibt man ca. 5 ml Spülmittel bzw. Shampoo, eine 10%ige Kaliumiodid-Lösung als Katalysator und mehrere Tropfen Wasserstoffperoxid (H2O2). Nun wird der Standzylinder leicht geschüttelt.
| Beobachtung: | Der Schaum in dem Zylinder steigt nach oben. |
| Erklärung: | Durch das H2O2 gibt es eine Sauerstoffentwicklung. Dadurch werden die Seifenblasen aufgeblasen. |


| 16-2. Seifenblasenautomat | zum Seitenanfang  |
An einem Strohhalm wird ein Luftballon befestigt, der durch den Strohhalm anschließend aufgeblasen wird. Nun wird der Strohhalm in ein mit Seifenblasenlösung befülltes Gefäß gesteckt.
| Beobachtung: | Viele kleine Seifenblasen blubbern von ganz alleine aus dem Gefäß. |
| Erklärung: | Die Luft strömt aus dem Ballon und bläst die Blasen auf. |

| 16-3. Riesenseifenblasen | zum Seitenanfang  |
Der Unterschied von Riesenseifenblasen zu "normalen" Seifenblasen liegt nur in der Größe und dass der Umgang mit ihnen nicht so leicht ist. Bei Riesenseifenblasen ist es ratsamer wenn man nicht in den Pustering pustet, sondern ihn durch die Luft schwingt. Um die Blase abzulösen macht man eine leichte Kreisbewegung.
Um zu gewährleisten dass die Blasen stabil werden muss die Lösung mindestens 4 Stunden stehen gelassen werden.

| 17. Seifenblasenshows | zum Seitenanfang  |
Seifenblasen faszinieren alle. In vielen Shows werden Kinder und Erwachsene in den Bann dieser schillernden Wunderkugeln gezogen. Von Riesenseifenblasen in die Menschen und teilweise sogar ganze Autos gestellt werden, über rauchgefüllte Seifenblasen, bis hin zu den unglaublichsten Dingen die man mit ihnen machen kann, wird alles gezeigt.
| 18. Zusammenfassung / Summary | zum Seitenanfang  |
Zusammenfassung
Seifenblasen gibt es seit Entdeckung der Seife durch die Sumerer. Sie bestehen grundsätzlich aus: Wasser, Tensiden (zum Herabsetzen der Oberflächenspannung) und Verdickungsmittel (Glycerin, Zucker, Maissirup). Sie entstehen hauptsächlich durch die Tenside, welche die Oberflächenspannung des Wassers herabsetzt. Die Farbe entsteht dadurch dass das Licht teilweise gebrochen und teilweise reflektiert wird. Sie sind nicht sehr lange haltbar da das Wasser den Erdanziehungskräften unterliegt und so die Seifenblasenhaut im oberen Teil sehr schnell, sehr dünn wird. Außerdem verdunstet das Wasser seht schnell.
Seifenblasen sind Kugeln, da dies die Prinzipien des Minimalflächenprinzips erfüllt: Die kleinste Fläche mit größtmöglichem Volumen zu erreichen.
Pusteringe können mit Draht und Wolle selbst hergestellt werden.
Seifenblasen werden in der Wissenschaft genutzt um schwierige räumliche Probleme zu lösen.
Bei meinen Versuchen testete ich verschiedene Seifenlösungen und variierte die Konzentrationen. Mit der Lösung die, die besten Seifenblasen ergab wurden auch physikalische Versuche durchgeführt, wie das Minimalflächenprinzip, die Oberflächenspannung oder der Druck in einer Seifenblasen. Für die Riesenseifenblasen wurde eine andere Lösung verwendet, da diese in größeren Mengen hergestellt werden musste.
Summary
Soap bubbles is fun for old and young, existing since the discovery of soap.
Fundamentally they consist of:
Water, tensids and enthickeners.
Soap bubbles are caused by the special arrangement of the tensids which reduce the water's surface tension by their charge and capture it by the forming of the bubble. Their colours are caused by refraction and the different reflexion of the sunlight. The reason why they burst so fast can be explained by the fact that the water between the tensids is attracted by gravity and so the bubble's skin on the upper side gets to thin. Frames can be built easy by wire and wool.The skin which occurs in the ring can be blown out or pulled through the air.
In science soap skins are used for testing difficult roof constructions. They are also used in the therapy of ill people.
Soap bubbles are spheres, because a sphere forms the smallest surface. When I produced and tested different soap solutions I discovered a very good consistence, containing washing up liquid which has tensids. I Also varied the enthickeners and concentrations of the solutions. Furthermore I did some show experiments and some physically experiments.
| 19. Literatur- und Bezugsquellen, Abbildungsverzeichnis | zum Seitenanfang  |
| Literaturquellen | zum Seitenanfang  |
Geschichte der Seifenblasen:
www.pustefix.de (11.08.05)
Buch: Michael Schuyst "Seifenblasen. Schwebende Träume - Kugeln der Götter" Du MontEntstehung von Seifenblasen:
www.Die-Chemie-der-Seifen-und-Waschmittel.de
www.klaus-groth-schule.de (11.08.05)
www.experimentalchemie.de (11.08.05)
www.wikipedia.org (11.08.05)Farben von Seifenblasen:
www.experimentalchemie.de (10.10.05)
www.wikipedia.org (10.10.05)
Microsoft Encarta 2005Warum zerplatzen Seifenblasen?:
www.allesüberseifenblasen.de (11.08.05)
www.experimentalchemie.de (10.10.05)
www.wikipedia.org (10.10.05)
www.klaus-groth-schule.de (10.10.05)Gestelle für Seifenblasen:
www.science-days.de (11.08.05)
www.chs.asn-graz.ac.at (10.10.05)
www.pustefix.de (11.08.05)
www.lo-net.de (11.08.05)
www.wikipedia.org (11.08.05)
www.hobbythek.de (11.08.05)Seifenblasen & Mathematik:
www.einstein-und-die-Seifenblasen.de (05.01.06)
www.wikipedia.org (05.01.06)Seifenblasen & Wissenschaft:
www.expo2000.de (04.01.06)
www.uni-paderborn.de (04.01.06)Seifenlösungen:
www.experimentalchemie.de (11.08.05)
www.hausfrauenseite.de (10.10.05)
www.wikipedia.org (10.10.05)
www.klaus-groth-schule.de (11.08.05)
www.lo-net.de (19.11.05)
Buch: Michael Schuyst "Seifenblasen. Schwebende Träume - Kugeln der Götter" Du MontMinimalflächenprinzip:
www.uni-paderborn.de
www.klaus-groth-schule.de
www.contets.de
www.wikipedia.org
www.uni-stuttgart.deOberflächenspannung:
www.uni-paderborn.de (11.08.05)
www.klaus-groth-schule.de (11.08.05)
www.wikipedia.org (11.08.05)Druck in einer Seifenblase:
Einfache Experimente mit Seifenblasen, chemisch didaktische Perspektiven (20.11.05) Viktor ObendraufAnwendungsversuche:
Einfache Experimente mit Seifenblasen, chemisch didaktische Perspektiven (20.11.05) Viktor Obendrauf
| Bezugsquellen | zum Seitenanfang  |
Spülmittel, Neutralseife, Shampoo, Strohhalme, destilliertes Wasser:
Schlecker, d&mGlycerin:
ApothekeTapetenkleister, Draht, Wollfaden:
Bastelladen"IDEE", Creativmarkt, Kronenstr. 4, Stuttgart-MitteMaissirup:
www.raabvitalfood.comLuftballons, fertige Pusteringe:
KinderspielzeugwarenladenVentile, Schlauch:
Gartenmarkt (Gardena)Puderzucker, Zucker:
von zu Hause
| Abbildungsverzeichnis | zum Seitenanfang  |
- Abb. 1 "Seifenbläser" ("Jean-Baptiste Siméon Chardin 022.jpg") Autor: Jean-Baptiste Siméon Chardin
Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Jean-Baptiste_Siméon_Chardin_022.jpg - Abb. 11 "Farbkreis nach Johannes Itten (1961)" © Malte Ahrens
Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Farbkreis_Itten_1961.png - Abb. 13 "Two soap bubbles" ("Soap Bubble - foliage background - iridescent colours - Traquair 040801.jpg") © en:User:Tagishsimon
Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Soap_Bubble_-_foliage_background_-_iridescent_colours_-_Traquair_040801.jpg - Abb. 16 "Olympiahalle " © Radox
Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Olympiahalle.jpg - Abb. 18 "Struktur von Seifenblasen" © André Karwath aka Aka
Quelle: http://de.wikipedia.org/w/index.php?title=Bild:Foam_-_big.jpg - Abb. 23: www.uni-stuttgart.de/minimalflächen.html
- Abb. 24, 28, 29, 30, 31, 33, 34, 35, 36, 37, 38: Myriam Petit
- Abb. 39: www.uni.stuttgart.de/Vorlesungsversuche/Oberflaechenspannung.html
- Abb. 40, 41, 42: Myriam Petit
- Abb. 43: www.uni-stuttgart.de/vorlesungsversuche/Oberflaechenspannung.html
- Abb. 44, 45: Myriam Petit
- Abb. 46: www.uni-stuttgart.de/vorlesungsversuche/großeundkleineSeifenblase.html
- Abb. 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 58, 59, 60, 61: Myriam Petit
« zurück zur Übersicht - Projektarbeiten




